Module 4 - Detecting population structure using PCA

Workshop 3 - Training course in data analysis for genomic surveillance of African malaria vectors

Module 4 - Detecting population structure using PCA#

Theme: Analysis

In this module we’re going to investigate population structure by running principal components analysis (PCA) using genetic variation data from Ag3.0. We will use functions in the malariagen_data python package to run and plot PCAs, then learn how interpret the results to discover taxonomic and geographic structure in mosquito populations.

Learning objectives#

At the end of this module you will be able to:

Compute principal component analyses across different mosquito cohorts.
Plot variance and principal components and interpret results.
Discover taxonomic and geographic population structure.

Lecture#

English#

Français#

Please note that the code in the cells below might differ from that shown in the video. This can happen because Python packages and their dependencies change due to updates, necessitating tweaks to the code.

Recap: what is population structure?#

In Ag3.0 there are 2,784 wild-caught mosquitoes collected from 19 countries in sub-Saharan Africa. This includes mosquitoes from three known species within the Anopheles gambiae species complex. When we have a cohort of mosquitoes from different species and/or geographical locations, we would expect that not all mosquitoes are equally closely related to each other. These non-random patterns of relatedness are known as population structure.

For example, we might expect that any two mosquitoes from the same species will be more closely related than two mosquitoes from different species. This will hopefully be intuitively obvious, because mosquitoes will prefer to mate with individuals of the same species, even if they live alongside mosquitoes from other species and can hybridise. This is also known as reproductive isolation and it may be caused by different drivers, e.g., behavioural differences leading to a lower likelihood of mating.

Similarly, we might expect that two mosquitoes sampled from the same location will be more closely related than two mosquitoes sampled from distant locations. This is based on the assumption that mosquitoes may travel to find a mate, but may only be willing or able to travel a certain distance. Mosquitoes may also be impeded from travelling in certain directions by natural physical barriers, such as a region of elevated terrain, or by variation in the availability of suitable habitat. These limits and barriers to movement can thus generate population structure, also known as geographic isolation.

For both of these causes of population structure – reproductive isolation and geographical isolation – we may have some idea of what to expect based on our knowledge of previous studies, but we may be surprised.

For example, the Anopheles gambiae species complex continues to be unravelled, and there may be cryptic species that we were not previously aware of (e.g., see Crawford et al. 2016 and Tennessen et al. 2020). We will return to this topic with an entire workshop about discovering cryptic species.

Also, recent studies have suggested that some malaria mosquitoes may engage in long-distance migration (Huestis et al. 2019), challenging the previous view that mosquitoes generally don’t travel more than a few kilometres in their lifetimes (Service 1997). But we still don’t know to what extent long-distance migration occurs, or whether the rate or range of migration varies between geographical regions and/or mosquito species. We would also like to learn more about how ecological and landscape variation affects the movement and interbreeding of mosquito populations in different regions of Africa.

In short, we would like to investigate population structure, and we can use genetic variation data to do that. There are various methods for analysing population structure, but this module will focus on just one of these methods, principal components analysis (PCA). PCA is attractive because it is model-free, meaning that you don’t need to specify any model of population structure before-hand, you can just run PCA and start exploring the results. On the other hand, interpreting PCA requires some care, which we’ll expand on a little below. If you’re interested in reading more deeply about using PCA for investigating population structure, Patterson et al. (2006), Novembre and Stephens (2008) and McVean (2009) are all great resources.

Recap: what is PCA?#

In this workshop we’ve seen some examples of PCA being used to identify genetic structure in a group of samples and we’ve heard why being able to detect structure is useful for genomic surveillance and vector control, but what is a PCA actually doing to our data.

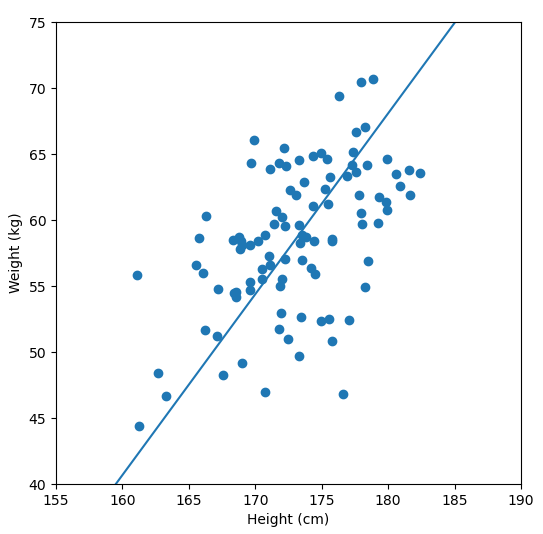
Fundamentally, PCA is a method for reducing the dimensions of a dataset to help make interpreting the data easier. A very simple example of what we mean by dimensions, one which we wouldn’t need PCA for, is a dataset in which each sample has two dimensions “weight” and “height”. With two dimensions we might be able to detect a relationship between them by looking at a scatter plot of the data, but what if a dataset had many more dimensions?

We are are interested in detecting population structure in a region of genomic data (e.g. a chomosome arm) which might have millions of SNPs (from hundreds or thousands of samples). Each consecutive genomic position in the dataset adds another dimension, so we can no longer easily compare the relationship of every dimension to every other dimension, like we could with our “weight” vs. “height” data example. Instead we use PCA to project principal components, which are similar to lines-of-best-fit, through our multi-dimensional data.

PC1, the first principal component, is the axis which describes the most variance in our data. All samples receive a single value for PC1 which describes their position along this axis. PC2 is the axis which describes the next most variance, and so on. A dataset with 100,000 dimensions can generate 100,000 principal components, but as much of the variance is explained (reduced) to the first few PCs we only need these to look for relationships. In our case, these relationships are population structure.

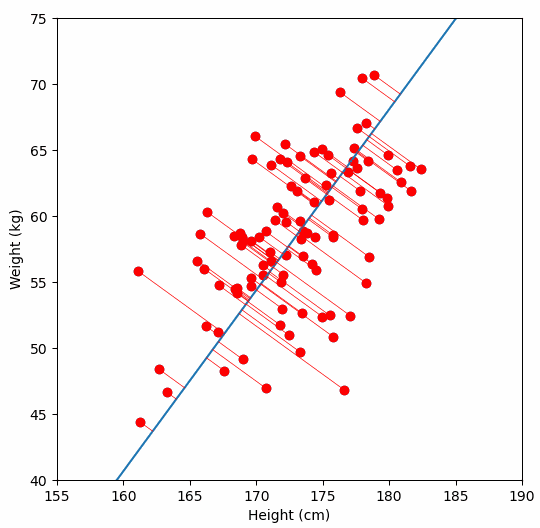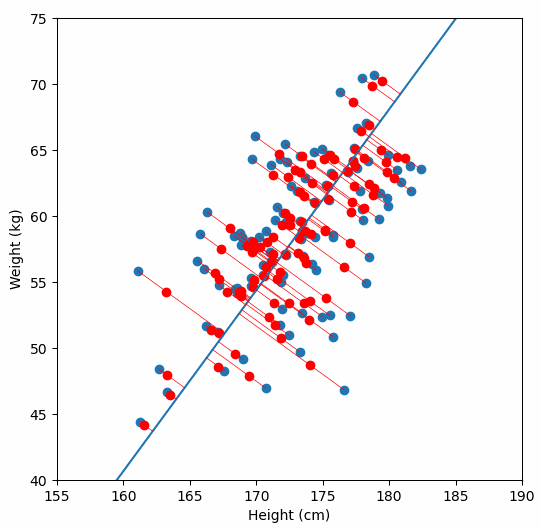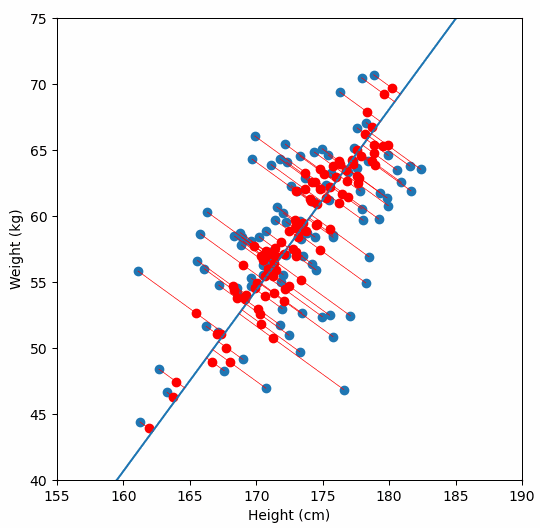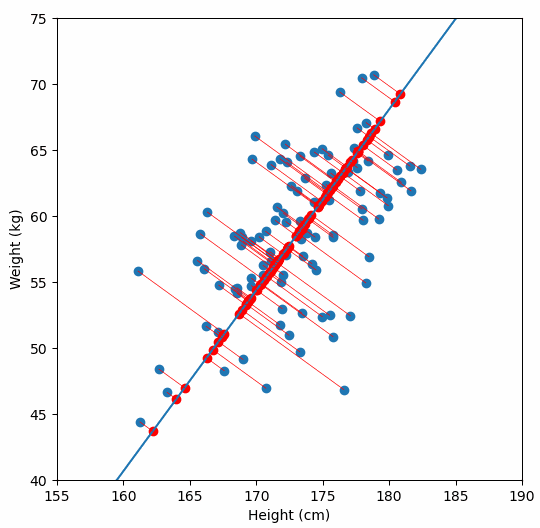
For a deeper dive into how PCA works, Bill Connelly’s blog post is excellent.

Behind the scenes of the `ag3.pca()` function#

Here’s what’s happening behind the scenes when we run the ag3.pca() function…

Access the genotypes that we would like to run the analysis on from Google Cloud Storage - which sample_sets, which region of the genome, and apply any sample_query included in the parameters (we will look at this functionality a bit later).
Allele count - this is the count of the alternate alleles for each site in the selected genomic region, across our samples. We are interested in sites where there is variation in our samples, known as segregating sites, particularly biallelic sites including the reference allele (i.e. where there is one alternate allele). These are the data upon which the PCA is run.
Thin the allele count - With ag3.pca() we can run a PCA analysis on entire chromosome arms, which contain millions of genomic positions. However, we can get strong signals of structure by using just a subset our segregating sites, plus if we used all the sites would make our analysis very slow. The n_snps parameter is used to ‘thin’ our SNPs. we find that around 100,000 SNPs is more than enough for analysis of population structure.
Run the PCA!

Setup#

Now that we have covered some of the theoretical background for population structure analyses using PCA, let’s install and import the python packages we will need for our analyses.

%pip install -q --no-warn-conflicts malariagen_data==9.0.0

Note: you may need to restart the kernel to use updated packages.

Note that authentication is required to access data through the package, please follow the instructions here.

import malariagen_data

import os
import plotly.express as px

Saving PCA results#

Some PCA runs may take a while to complete, particularly if you’re running this code on a service with modest computational resources such as Google Colab, because genotype calls from tens of millions of SNPs may need to be scanned to identify and extract the data for PCA. The run time will depend on the number of samples included in the analysis, but may take 20 mins or more for larger analyses.

To avoid having to rerun these analyses, we’ll save the results so we can come back to them later. In Google Colab, you can save results to your Google Drive, which will mean you don’t lose results even if you leave the notebook and come back several days later.

When mounting your Google Drive you will need to follow the authorization instructions.

try:
    # if running on colab, mount Google drive
    from google.colab import drive
    drive.mount('drive')
except ImportError:
    pass

With our Google Drive now mounted, we can define and make a directory where we want to save our PCA results.

results_dir = "drive/MyDrive/Colab Data/ag3-pca-results"
os.makedirs(results_dir, exist_ok=True)

In Google Colab, we can actually see our mounted drive and PCA results directory by clicking on the file tab on the left hand side of the screen.

Next we should setup the malariagen_data package. As we want to save our PCA results in the Google Drive folder we just set up, we’ll use the results_cache parameter and assign our results directory to it. If we were running this notebook locally, then we could assign a local folder to this parameter and the PCA results would instead get stored on our hard drive.

ag3 = malariagen_data.Ag3(results_cache=results_dir)
ag3

MalariaGEN Ag3 API client
Please note that data are subject to terms of use, for more information see the MalariaGEN website or contact support@malariagen.net. See also the Ag3 API docs.
Storage URL	gs://vo_agam_release/
Data releases available	3.0, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9
Results cache	/home/jonbrenas/anopheles-genomic-surveillance.github.io/docs/workshop-3/drive/MyDrive/Colab Data/ag3-pca-results
Cohorts analysis	20240418
AIM analysis	20220528
Site filters analysis	dt_20200416
Software version	malariagen_data 9.0.0
Client location	unknown

The output of ag3 shows us the “Client location”. This is where our Google Colab virtual machine is running on the cloud. As the data we would like to analyse is located in the US, it is worth checking that our notebook is running there too. If not, click “Runtime > Disconnect and delete runtime” from the menu, then re-run the notebook and check again.

Analysis: Central African Republic#

Now we’ve set up our environment and understand a bit more about PCA, we should run an analysis.

As discussed earlier, there a multiple steps involved in running a PCA analysis, but for convenience, we have combined these into a malariagen_data function called ag3.pca(). Before we start, let’s have a quick look at the documention using “?”

ag3.pca?

We can see that there are two required parameters:

region is one we are probably getting familar with by now, it defines what region of the genome we want to run the analyses over. We could assign a whole chromosome arm, a chromosome region, with a start and stop point, or a specific gene of interest.
n_snps requires us to define how many SNPs we would like to thin our region down to, as PCA doesn’t require every SNP (plus without thinning it could potentially take a very long to run the analysis).

Today we are going to run the PCA on a section of the 3L chromosome arm. 3L is a good choice of chromosome arm when looking at population structure, as results are not confounded by the large inversions that are found on 2L, 2R, 3R and X.

We’ll thin the SNPs on 3L down to around 100,000 as that should be plenty to see signals of structure, and rather than looking at all the Ag3.0 data, let’s use the sample_sets parameter to just look at the Central African Republic.

region = "3L:15,000,000-41,000,000"
n_snps = 100_000
sample_sets = "AG1000G-CF"

The ag3.pca() function actually returns two values, so we need to assign two variables when we run it.

pca_df, evr = ag3.pca(region=region, n_snps=n_snps, sample_sets=sample_sets)

Plotting principal components#

Let’s have a look at the pca_df output. It’s a Pandas DataFrame with one row per sample.

pca_df.head()

	sample_id	partner_sample_id	contributor	country	location	year	month	latitude	longitude	sex_call	...	PC11	PC12	PC13	PC14	PC15	PC16	PC17	PC18	PC19	PC20
0	BK0001-C	RCA_1	Alessandra della Torre	Central African Republic	Bangui	1993	12	4.367	18.583	F	...	-37.083614	-9.189623	101.646721	-71.306137	-76.473549	-36.296165	42.778328	-131.277283	-115.088371	83.109093
1	BK0002-C	RCA_2	Alessandra della Torre	Central African Republic	Bangui	1993	12	4.367	18.583	F	...	2.149113	-15.093954	60.621552	-22.569653	-35.937469	-18.220644	-3.786955	-24.488905	-11.645450	4.739120
2	BK0003-C	RCA_3	Alessandra della Torre	Central African Republic	Bangui	1993	12	4.367	18.583	F	...	-22.997334	-25.280819	3.785538	41.063396	-21.379868	16.304289	-2.194442	27.389791	10.179262	-47.615044
3	BK0005-C	RCA_5	Alessandra della Torre	Central African Republic	Bangui	1993	12	4.367	18.583	F	...	4.713781	-55.518913	-35.603748	-53.445442	-48.714108	9.790788	-0.997970	4.775346	8.943587	21.263462
4	BK0006-C	RCA_6	Alessandra della Torre	Central African Republic	Bangui	1993	12	4.367	18.583	F	...	-8.889878	44.444214	0.284841	8.827749	3.919391	-27.088953	-22.904848	4.395884	-36.892990	25.838764

5 rows × 52 columns

There are 52 columns, so we can’t fit them all our screen. If we access the column headers we can see that the first 31 columns are all metadata relating to the mosquito sample, e.g. its sample ID, collection site, taxon, etc.

pca_df.columns

Index(['sample_id', 'partner_sample_id', 'contributor', 'country', 'location',
       'year', 'month', 'latitude', 'longitude', 'sex_call', 'sample_set',
       'release', 'quarter', 'study_id', 'study_url',
       'aim_species_fraction_arab', 'aim_species_fraction_colu',
       'aim_species_fraction_colu_no2l', 'aim_species_gambcolu_arabiensis',
       'aim_species_gambiae_coluzzii', 'aim_species', 'country_iso',
       'admin1_name', 'admin1_iso', 'admin2_name', 'taxon',
       'cohort_admin1_year', 'cohort_admin1_month', 'cohort_admin1_quarter',
       'cohort_admin2_year', 'cohort_admin2_month', 'cohort_admin2_quarter',
       'PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6', 'PC7', 'PC8', 'PC9', 'PC10',
       'PC11', 'PC12', 'PC13', 'PC14', 'PC15', 'PC16', 'PC17', 'PC18', 'PC19',
       'PC20'],
      dtype='object')

If we use the .groupby function we can see that all samples were collected from a single location over two consecutive years.

pca_df.groupby(["country", "location", "year"]).size()

country                   location  year
Central African Republic  Bangui    1993     7
                                    1994    66
dtype: int64

The last 20 columns, all beginning “PC…”, are the results of our PCA analysis. For each sample we have generated a value for each of 20 principal components. We could return results for more or less principal components using the n_components parameter in ag3.pca(), but 20 is a good starting point.

We can examine these principal components and look for population structure in our dataset, by plotting one against another. As we know, the components are ordered by how much variance in the data they explain, so let’s look at PC1 and PC2 first.

We can use plotly express to make a simple scatter plot of these principal components.

fig = px.scatter(pca_df, x="PC1", y="PC2")
fig.show()

Each point here is a sample, so we can see that PC1 pulls apart two large clusters of samples and PC2 separates out two samples. Though this plot is informative, we could add some more data to make it easier to interpret. For example if we coloured the points by taxon, we could spot if any clustering is being potentially driven by reproductive isolation between species.

We could add more parameters to our plotly express argument above to achieve this, but to streamline our analysis process we have added a function within malariagen_data called ag3.plot_pca_coords() that will do this for us.

ag3.plot_pca_coords?

The documentation shows us that the only required parameter is our PCA output data. We’re going to also use the optional parameter color to pick the taxon column to define point colour.

ag3.plot_pca_coords(
    pca_df,
    color="taxon",
)

By colouring the points according to taxon we can now see that PC1 is pulling apart samples according to whether they are Anopheles gambiae or coluzzii, which is what we might expect of samples collected in the same place at a similar time but that are reproductively isolated as they are different species.

These plotly plots are interactive, if we hover over a sample’s point we can see a lot of useful metadata (compare this to the simple plotly express plot we made earlier).

Exercise 1 (English)

Run the same analysis on the Central African republic sample set, but this time look at the “2L” chromosome arm region instead of “3L”. Keep all the other parameters the same. Is the PC1 vs. PC2 scatter plot different when we look at “2L”? If so, what might be causing this?

Exercice 1 (Français)

Exécuter la même analyse de l’ensemble d’échantillons de la République Centrafricaine mais regarder cette fois le bras de chromosome “2L” au lieu de “3L”. Garder tous les autres parametres identiques. Est-ce que le diagramme à nuage de points entre PC1 et PC2 ressemble à celui au-dessus? Si non, quelle peut-être la raison?

# region_ex1 = "2L"
# n_snps_ex1 = ???
# sample_sets_ex1 = ???

# pca_ex1_df, evr_ex1 = ag3.pca(region=region_ex1, n_snps=n_snps_ex1, sample_sets=sample_sets_ex1)

# ag3.plot_pca_coords(
#     pca_ex1_df,
#     color="taxon",
# )

Plotting explained variance#

Let’s now have a look at the evr output. We can see that this is an array of 20 floats (numbers with decimal points). These are the percentage of variance in the dataset explained by each of our 20 principal components.

evr

array([0.02112054, 0.01766533, 0.01468957, 0.01466229, 0.01458635,
       0.01448812, 0.01446008, 0.0144149 , 0.01437675, 0.01432975,
       0.01428596, 0.01426135, 0.01423304, 0.01422987, 0.01421792,
       0.01419417, 0.01415763, 0.0141159 , 0.01410521, 0.01409187],
      dtype=float32)

If we look at our scatter plot of the 3L chromosome arm, it is clear that some of the An. gambiae samples spread out along PC2. How do we know whether this is meaningful or just random noise? Should we also investigate the higher principal components e.g. PC3 vs. PC4? One way to get an intuition for this is to examine the variance explained by each of the components.

The easiest was to do this is to plot our evr array in the form of a bar chart. We have a handy function in malariagen_data to do this for us. Again, this is an interactive plot and hovering the pointer over a bar will reveal the exact explained variance percentage.

ag3.plot_pca_variance(evr)

The first principal component explains around 2.5% of the variance, whereas all of the subsequent principal components explain around 1.5% of the variance. The absolute magnitude of these values is less important as this will change depending of what dataset we analyse. What is more important, however, is the fact that PC1 relatively explains much more variance than all the subsequent PCs. In other words, there is a big step down from PC1 to PC2, then the variance explained flattens off. This is a good indication that PC1 is capturing some real structure in the data, and the rest of the PCs are probably random noise.

There are various statistical methods for formally testing whether a principal component conveys a real signal of population structure or is just random noise (for example see Patterson et al. 2006 and Forkman et al. 2019). However, for exploratory analyses, looking at the differences in variance explained between the adjacent PCs, and ignoring the tail of PCs where the variance flattens off, is not a bad rule of thumb.

Interpretation: PCA and genetic distance#

In our scatter plot of PC1 and PC2, the An. coluzzii individuals all cluster close together. Similarly, most of the An. gambiae individuals cluster close together. It can be tempting to interpret this in the following way, which would be wrong:

“The individuals within each cluster are genetically nearly identical to each other.”

Similarly, it can be tempting to draw the following conclusion, which would also be wrong:

“The two clusters of individuals are genetically very different from each other.”

What is wrong with these statements?

In short, PCA does not tell you anything about the absolute magnitude of genetic distance between individuals. All it can tell you is something about relative genetic distance. The PCA tells us that the An. coluzzii individuals are more closely related to each other than to the An. gambiae individuals, and vice versa. However, it does not tell us how much more, and there may still be a lot of genetic diversity within each of these clusters.

The key point is that all individuals within each cluster are related (or unrelated) to each other by a similar degree.

We can see this in action if we compare these two PCA plots. The first is analysis of just the An. gambiae samples from Burkina Faso. The second is both the An. gambiae and An. coluzzii samples from the same country.

pcr_bfg_df, evr_bfg = ag3.pca(
    region=region,
    n_snps=n_snps,
    sample_sets=["AG1000G-BF-A", "AG1000G-BF-B", "AG1000G-BF-C"],
    sample_query="taxon == 'gambiae' and country == 'Burkina Faso'",
)

ag3.plot_pca_coords(
    pcr_bfg_df,
    color="taxon",
    title="Burkina Faso just An. gambiae"
)

pcr_bf_df, evr_bfg = ag3.pca(
    region=region,
    n_snps=n_snps,
    sample_sets=["AG1000G-BF-A", "AG1000G-BF-B", "AG1000G-BF-C"],
    sample_query="taxon in ['gambiae', 'coluzzii'] and country == 'Burkina Faso'",
)

ag3.plot_pca_coords(
    pcr_bf_df,
    color="taxon",
    title="Burkina Faso, An. gambiae and coluzzii"
)

As we can see from these two plots, the distance between the points is relative. In the first plot, An. gambiae samples are spread across PC2 and and a single sample, AB0325-C, is driving clustering on PC1. However, in the second plot the same samples are much more tightly clustered with PC1 now being driven by taxon and the gambiae outlier sample, AB0325-C, is now driving PC2.

Analysis: East African An. arabiensis#

We can also combine data from multiple countries to perform a broader analysis of population structure. Let’s run a PCA of some An. arabiensis mosquitoes from East Africa. This is a larger set of samples, so may take a little longer to run.

We’ll use the sample_query parameter to just analyse An. arabiensis from Tanzania, Kenya and Malawi.

pca_ea_df, evr_ea = ag3.pca(
    region="3L",
    n_snps=n_snps,
    sample_sets="3.0",
    sample_query="taxon == 'arabiensis' and country in ['Tanzania', 'Kenya', 'Malawi']",
)

ag3.plot_pca_coords(
    pca_ea_df,
    color="country",
)

By colouring the points according to country we can see that PC1 is separating samples from Malawi away from Tanzania and Kenya. What we are looking at here is most likely geographical isolation between Malawi and the more northerly countries Tanzania and Kenya.

There are a couple of Tanzanian samples that are separated along PC2. However, by plotting the variance explained by each principal component we can see that after PC1 the tail flattens off straight away, so the PC2 result is probably just noise.

ag3.plot_pca_variance(evr_ea)

Exercise 2 (English)

Run a PCA on An. gambiae from Uganda. Is there population structure here? It might be useful to colour the plot points by location, how would we do that?

Exercice 2 (Français)

Exécuter la PCA pour les An. gambiae venant de l’Uganda. Y a-t-il de la structure de population? Il peut être utile de colorer les points en fonction du lieu de capture.

# sample_query_ex2 = (???)

# pcr_ex2_df, evr_ex2 = ag3.pca(
#     region=region,
#     n_snps=n_snps,
#     sample_sets="3.0",
#     sample_query=sample_query_ex2
# )

# color_ex2 = '???'

# ag3.plot_pca_coords(
#     pcr_ex2_df,
#     color=color_ex2,
# )

Well done!#

In this module we have run principal component analyses across different mosquito cohorts, learned how to plot variance and principal components, and interpret results to discover taxonomic and geographic population structure.

Exercises#

English#

Open this notebook in Google Colab and run it for yourself from top to bottom. As you run through the notebook, cell by cell, think about what each cell is doing, and try the practical exercises along the way.

Have go at the practical exercises, but please don’t worry if you don’t have time to do them all during the practical session, and please ask the teaching assistants for help if you are stuck.

Hint: To open the notebook in Google Colab, click the rocket icon at the top of the page, then select “Colab” from the drop-down menu.

Français#

Ouvrir ce notebook dans Google Colab et l’exécuter vous-même du début à la fin. Pendant que vous exécutez le notebook, cellule par cellule, pensez à ce que chaque cellule fait et essayez de faire les exercices quand vous les rencontrez.

Essayez de faire les exercices mais ne vous inquiétez pas si vous n’avez pas le temps de tout faire pendant la séance appliquée et n’hésitez pas à demander aux enseignants assistants si vous avez besoin d’aide parce que vous êtes bloqués.

Indice: Pour ouvrir le notebook dans Google Colab, cliquer sur l’icône de fusée au sommet de cette page puis choisissez “Colab” dans le menu déroulant.

Further study#

If you’d like to continue with PCA and investigating population structure in the Anopheles gambiae complex, here are some suggestions for further analyses to run.

Investigate geographical population structure within each of the three main taxa represented in the Ag3.0 data release: An. arabiensis, An. coluzzii and An. gambiae.

Geographical population structure in An. arabiensis#

Below is a code example which runs a PCA on all An. arabiensis samples in the Ag3.0 data release. This will take a few minutes to run. Uncomment this code and try running it for yourself.

# pca_df_arab, evr_arab = ag3.pca(
#     region="3L:15,000,000-41,000,000", 
#     n_snps=100_000, 
#     sample_sets="3.0",
#     sample_query="taxon == 'arabiensis'"
# )

Uncomment and run the code cells below to plot the explained variance, and then visualise the first three principal components using a 3D scatter plot.

# ag3.plot_pca_variance(evr_arab)

# ag3.plot_pca_coords_3d(
#     pca_df_arab,
#     color="country",
#     title="PCA - An. arabiensis",
# )

How many distinct populations do you think there are?

Geographical population structure in An. coluzzii#

Adapt the code examples given above to run a PCA on all An. coluzzii samples in the Ag3.0 data release and then plot the results.

Try plotting more than just the first three principal components.

How many distinct populations do you think there are?

Geographical population structure in An. gambiae#

Now adapt the code examples given above to run a PCA on all An. gambiae samples in the Ag3.0 data release and then plot the results.

Again, try plotting more than just the first three principal components.

How many distinct populations do you think there are?

Module 4 - Detecting population structure using PCA

Contents

Module 4 - Detecting population structure using PCA#

Learning objectives#

Lecture#

English#

Français#

Recap: what is population structure?#

Recap: what is PCA?#

Behind the scenes of the ag3.pca() function#

Setup#

Saving PCA results#

Analysis: Central African Republic#

Plotting principal components#

Plotting explained variance#

Interpretation: PCA and genetic distance#

Analysis: East African An. arabiensis#

Well done!#

Exercises#

English#

Français#

Further study#

Geographical population structure in An. arabiensis#

Geographical population structure in An. coluzzii#

Geographical population structure in An. gambiae#

Behind the scenes of the `ag3.pca()` function#